プログラミングは、論理的な考え方をしなければならない?
みたいな発想はしなくても大丈夫です。自然に身についていくことです。
論理的な思考力とか、プログラミング的思考力ってよく聞くけれど・・・実際にどんな思考力なの?
っと、、、気になる方も多いですよね?
気にならないかな?
論理的思考力とは?
道理や筋道に則って思考を巡らせて結論を導いたり、
あるいは、複雑な事柄を分かりやすく説明したりできる能力として主に捉えられる。
英語の logical thinking(ロジカルシンキング)の訳語
といった説明が出てきます。(BY.weblio)
ということで、
プログラミングを義務教育で行う目的にもなっていることでしょう。
筋道に沿って思考を巡らせる。
これは、モノ作りにおいても、手順通りにしないと・・
ってことで、身についていく能力だと考えられます。
効率的にってことも含めて、というこは、おいといて、それじゃ何でプログラミングなの?
プログラミングって何がいいの?
といったことになりますよね
プログラミングを学ぶ利点としては?
効率的になるということもあります。
ただし、使い方を間違えると、、、
「あれ?」これじゃ意味ないじゃん。。。
みたいなことにもなりますので要注意です。
例えば、、、
ボールの動きを描くプログラミングを子ども向けのスクラッチで書くと
こんな感じになります。(見にくい場合は画像をクリックして下さい)
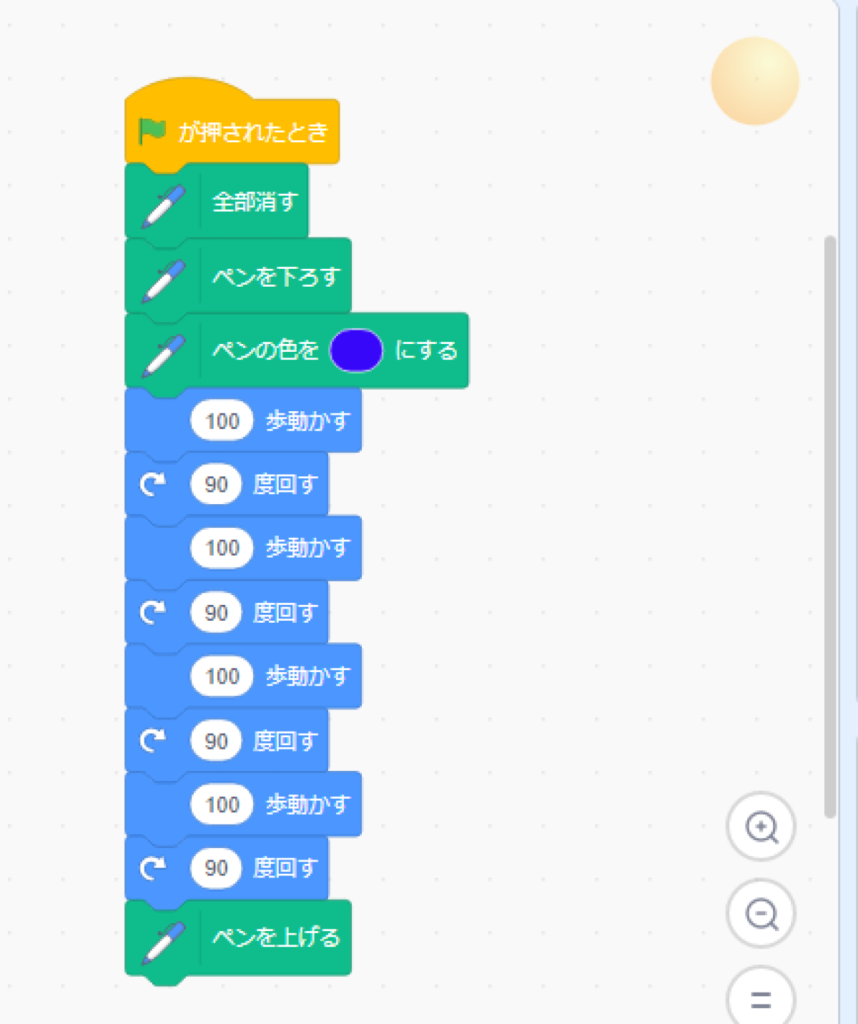
これで動かすと・・・
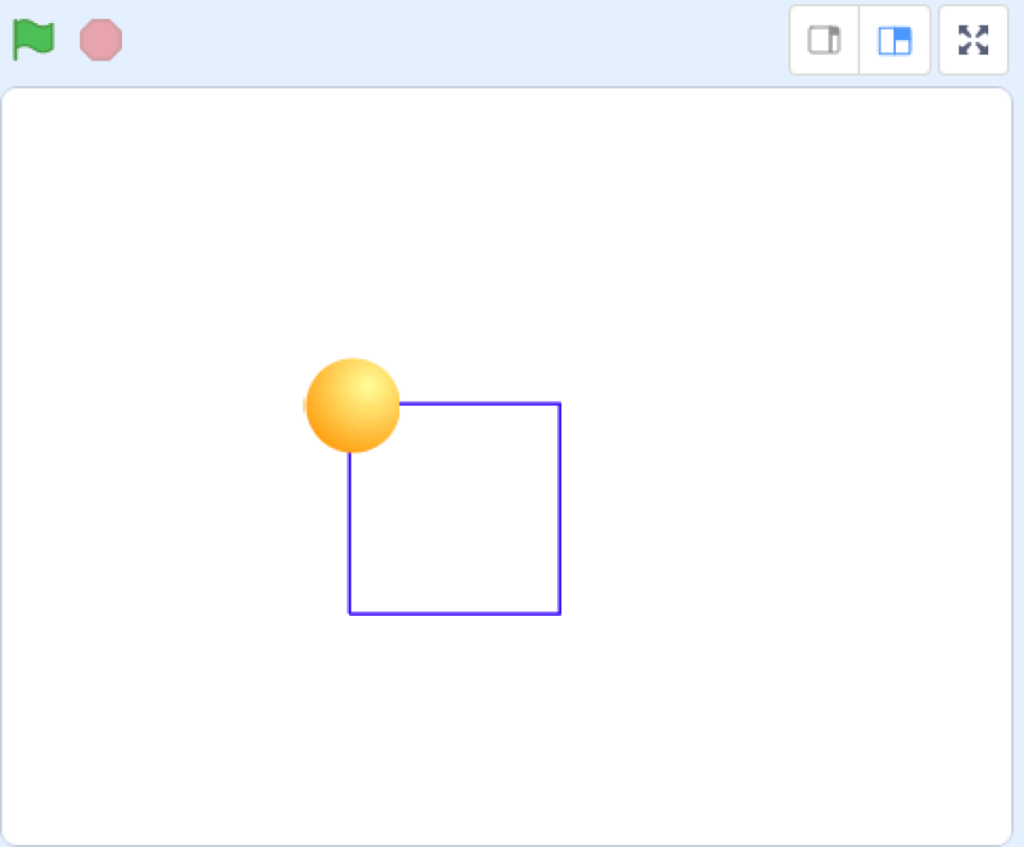
こんな感じになります。
で、このプログラミングは、正しいといった結果になります。
が・・・
このプログラミングは、NGなんです。
こんな作りをすることは、滅多にありません。(笑)
もう少しスッキリ、簡単に書けないかな?
っといったことを考えるのも、プログラミング的な思考力なんです。
どういうことか?
次に、三角形を描くように変えてみようか?
ってなった場合、、、
1っ個、消すの?
ということになります。
このプログラミングをこんな感じに作っていると、、、
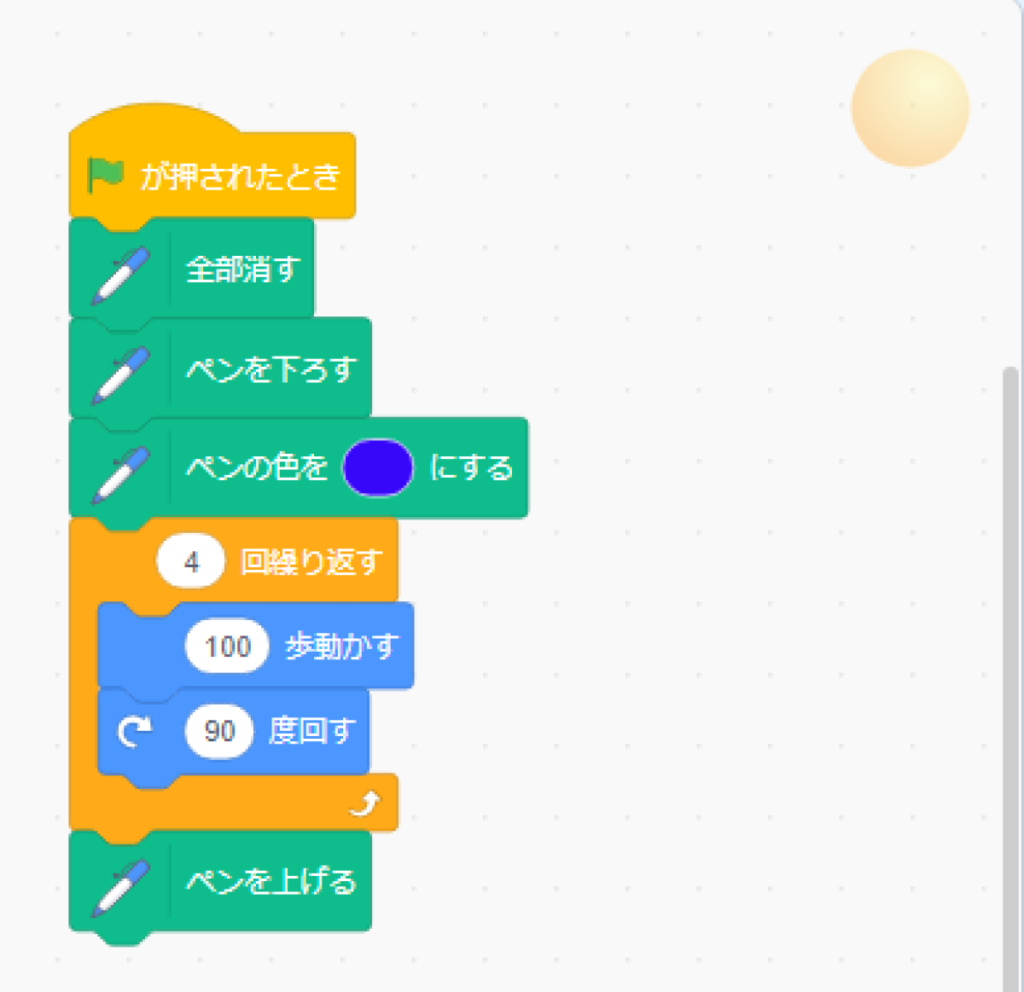
4回繰り返す箇所を3に、、、
90度まわすとこをXX度に・・・
といった感じで、、、修正も楽なんです。
また、関数としても作れますので、使いまわしができてきます。
このような発想になれば、プログラミング的な思考力が身についてきたといえることでしょう。
いかにスッキリしたプログラミングになるか?
誰が見ても解りやすく、ステップ数(行数)も少なくて済むか?
を考えるのもプログラミング的な思考力です。
簡単なプログラミングコードは、
よいプログラミングみたいに思われることも多いです。
だから
Python言語って注目されているんだと思います。
ステップ数が少なくて済むということは、
間違いがおこりにくい。見やすいプログラムともいえるんだから
記述する時間も少ないので、短時間でデキルっていうメリットもあるし・・・
実行スピードに関しては、遅いけど・・・
ということで、
三角形を描くのは、
120度回転にすればいいということで、、、
これは、単純にひっかけ問題。
三角形でしょ?だったら60度
って、なって、、、
60に直すんだ。
で、動かして・・・あれ?なんで?
って感じになる。
よかったら、試してくださいね
これイベントなどでよく使ってます。
試行錯誤ってことが、よく解ります。
だから、
プログラミングなんだ・・・ってことも
では、次に、こんな★を一筆書きで書かせて見て下さい。
これも、同じような感じで、
繰り返しの数と、角度、、
ちょっと、小さくなるので、歩数を増やすとできます。
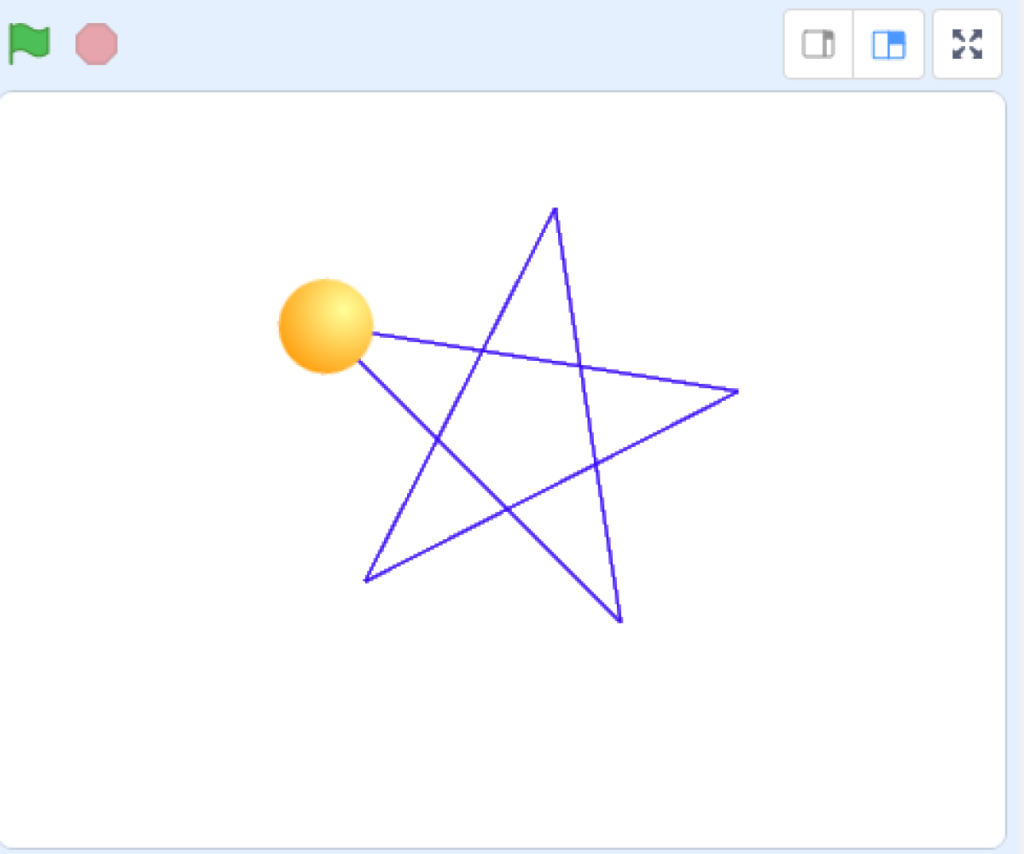
正解はこちらも
少し考えてみて下さいネ、、、二等辺三角形になっている部分と
中央が5角形になっていることに注目すると、
答えは出てきますよね?
ヒントとしては、正五角形の内角の和
三角形+四角形となるので、その一つの角度が・・・
みたいな感じで計算してみて下さいネ
これも問題として、やってみてね
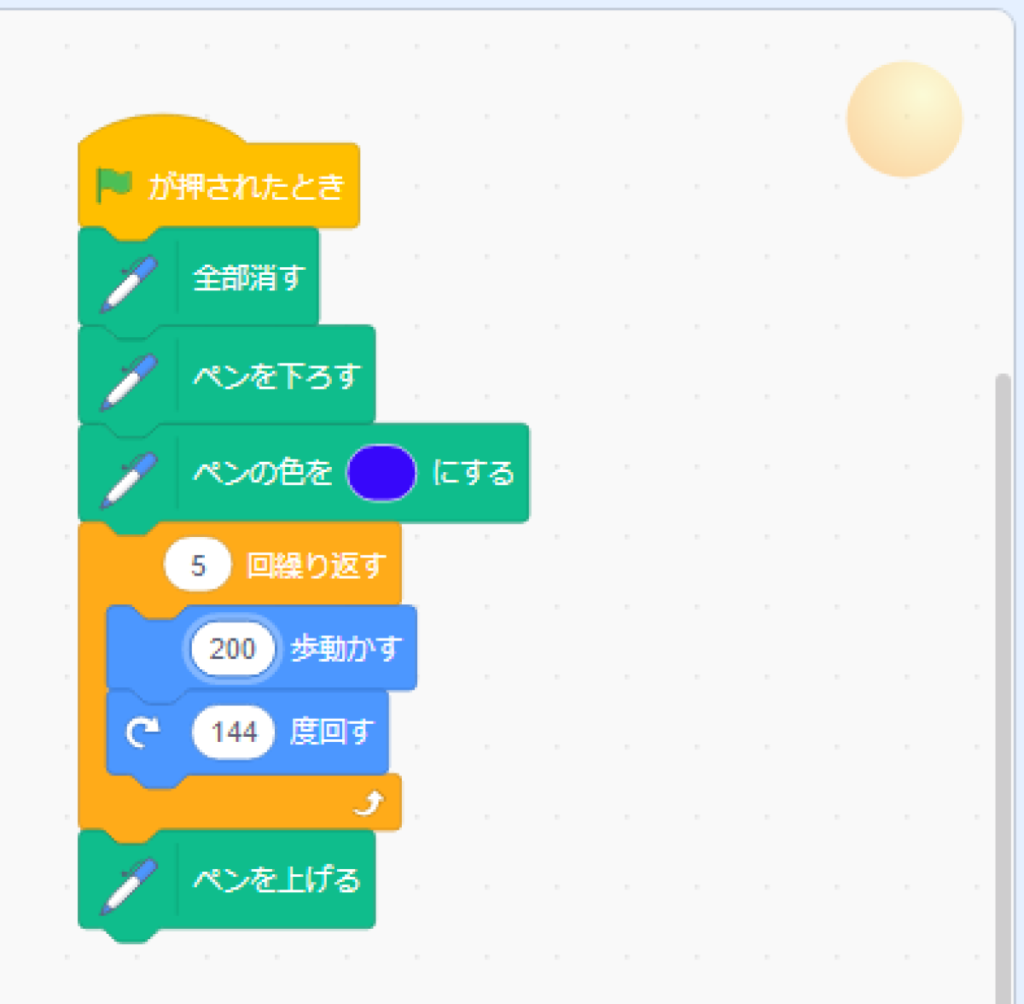
なんだ、3回や5回だけじゃん。
消したり、追加すりゃいいじゃん
みたいに思わるかも知れませんが・・・・
今度は、円を描いてみて下さい。
っとなると・・・
円だから、360度・・
1度を360回繰り返してみると・・・
みたいな発想になって、、、
あぁ、繰り返し使えば、いいんだな
ってことに気が付くかもしれない。
まさか、360個も並べて作るようなことはしないでしょ(笑)
実際に、作りながら学んでもらえればいいです。
なんで、繰り返しを使うのか?
って疑問に思って、、、実際に試して、気が付いて、、、
あぁ、ちょっとした修正で、終わるからか・・・
みたいに感じて頂ければいいです。
コピペして、値を少し変えるだけなんですよ。
使いまわしが出来るのもプログラミングのいいとこです。
だから、作ったコード、プログラミングコードは、資産になるんです。
著作権もあるし(笑)
ってことで、こんな円になります。
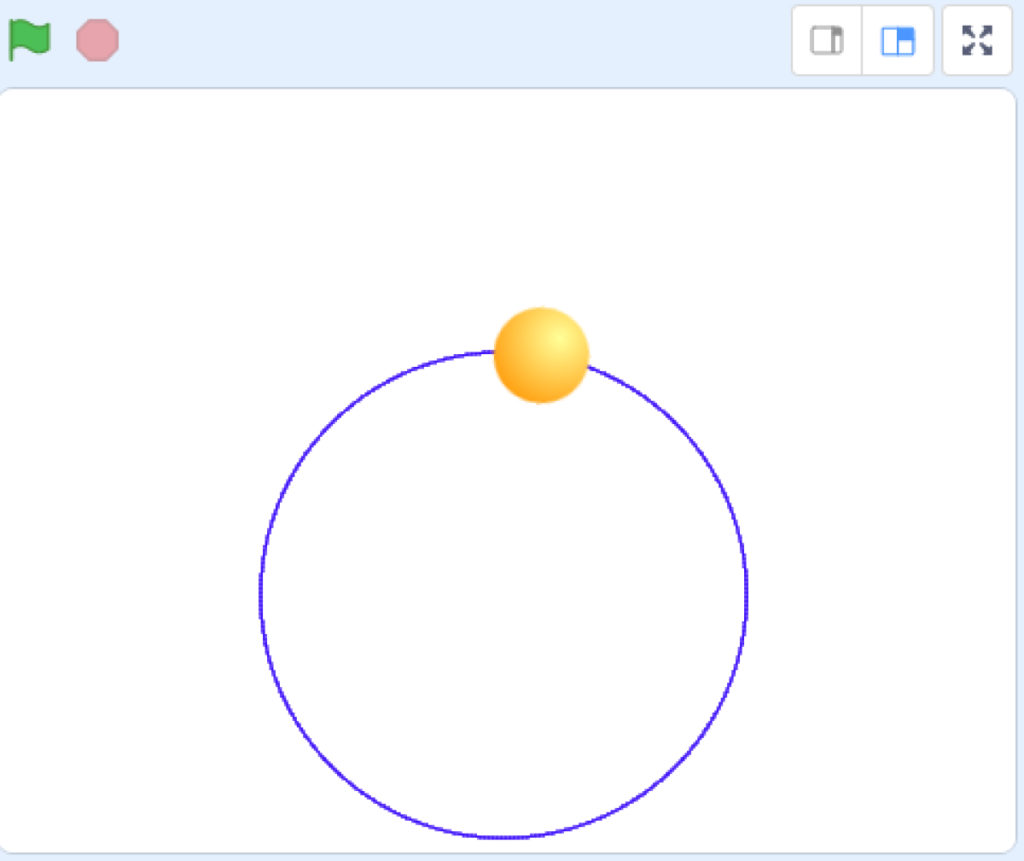
こんな感じに円が書ければOK
プログラミングコードは?
こんな感じ
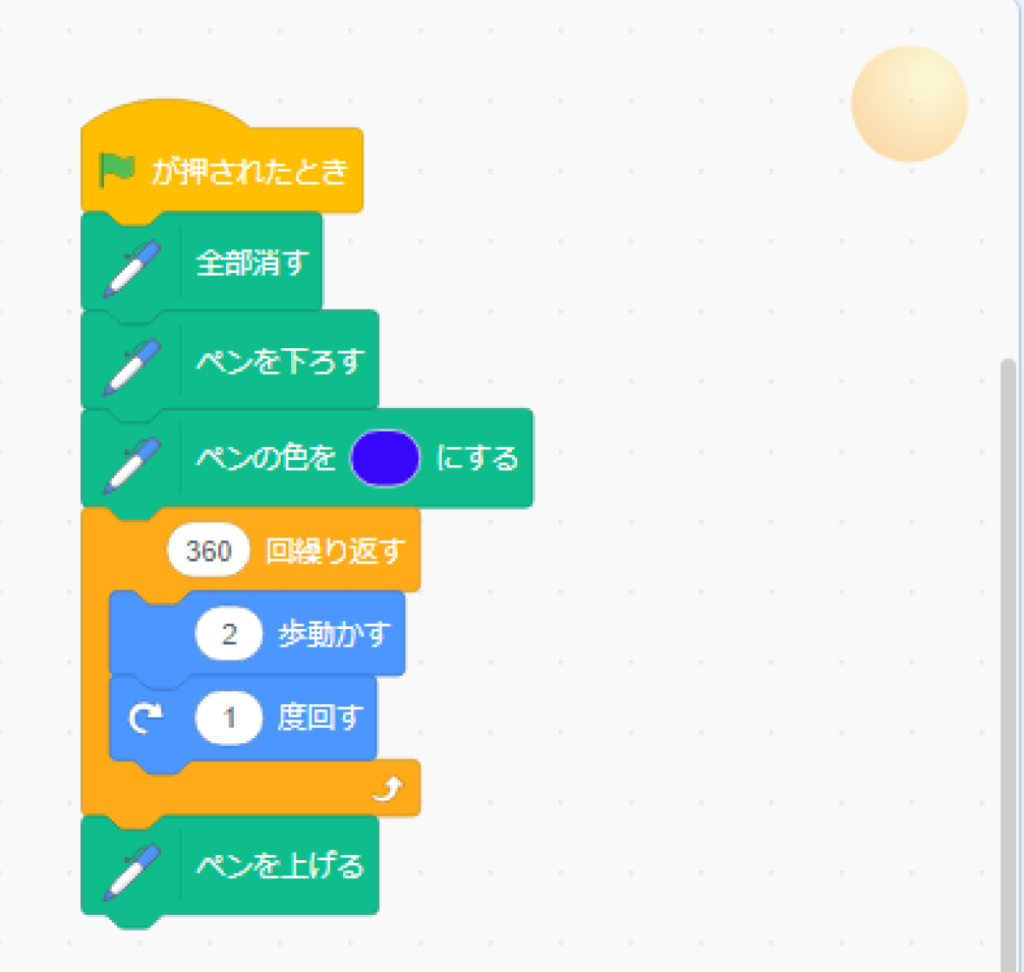
最初作った、4回繰り返す、四角形のプログラミングと同じです。
数値を修正するだけでいろいろ絵が描けました。
歩数を少なくしているのは、画面に収まる大きさにするためです。
面白いでしょ?
高校生?くらいになって、
Sin や Cos を習うと、使ってみるといいでしょう。
ホントに円になるの??みたいに
あまり自信ないけど、、、
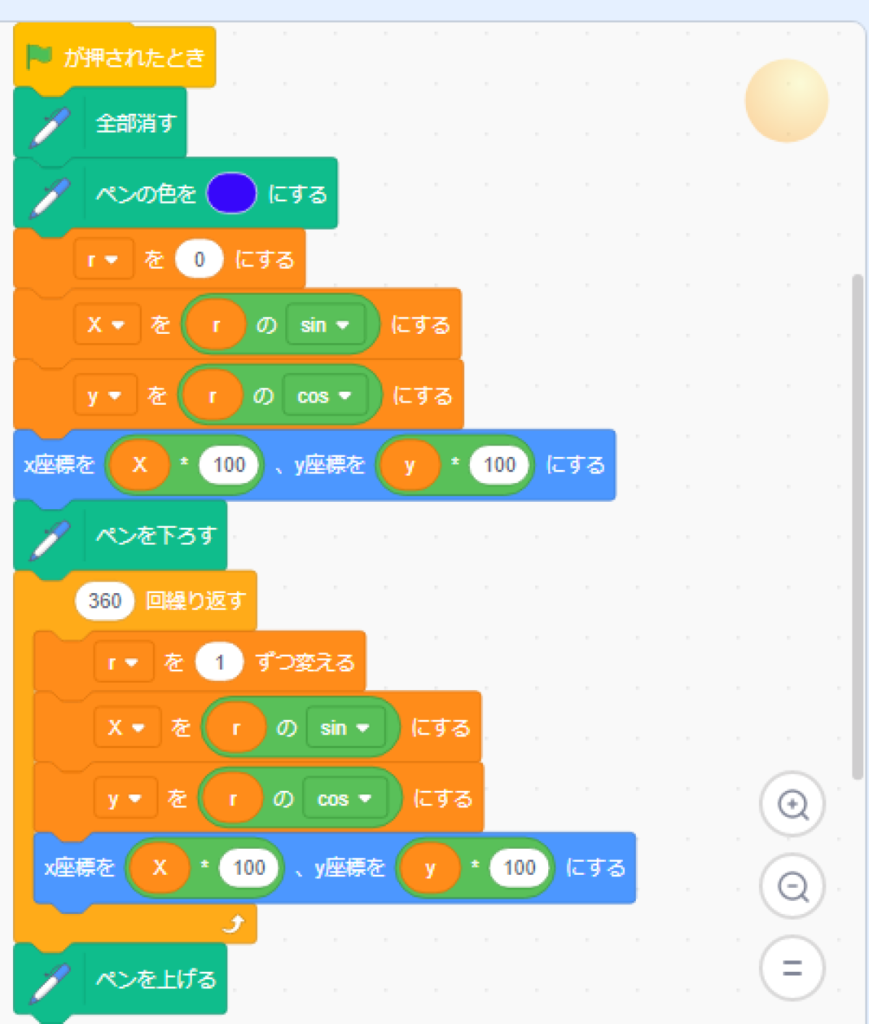
最初にX座標、Y座標をゼロ、ゼロの位置に
移動するためにちょっと小細工しています。
XとYが逆?sinとcosが逆?
sinがY座標でcosがX座標だから、逆でした。
m(__)m
どっちでも円になるけど・・・
X軸とY軸が逆になります。
もっと、効率よく使いまわしのできる仕組みってないのかな?
ここまでで完成としても問題もないのですが、もっと、効率よくを考え続けることも当然できます。
興味がありましたら、「関数(かんすう)」についてのお話も続けてごらんください。
事例も多いので、参考書的な本⇒スクラッチプログラミング事例大全集


